Escalas termométricas:

En todo cuerpo material la variación de la temperatura va acompañada de la correspondiente variación de otras propiedades medibles, de modo que a cada valor de aquélla le corresponde un solo valor de ésta. Tal es el caso de la longitud de una varilla metálica, de la resistencia eléctrica de un metal, de la presión de un gas, del volumen de un líquido, etc. Estas magnitudes cuya variación está ligada a la de la temperatura se denominan propiedades termométricas, porque pueden ser empleadas en la construcción de termómetros.

Escala Celsius

Una vez que la propiedad termométrica ha sido elegida, la elaboración de una escala termométrica o de temperaturas lleva consigo, al menos, dos operaciones; por una parte, la determinación de los puntos fijos o temperaturas de referencia que permanecen constantes en la naturaleza y, por otra, la división del intervalo de temperaturas correspondiente a tales puntos fijos en unidades o grados.

Escala Fahrenheit

En los países anglosajones se pueden encontrar aún termómetros graduados en grado Fahrenheit (ºF). La escala Fahrenheit difiere de la Celsius tanto en los valores asignados a los puntos fijos, como en el tamaño de los grados. Así al primer punto fijo se le atribuye el valor 32 y al segundo el valor 212. Para pasar de una a otra escala es preciso emplear la ecuación:

t(ºF) = 1,8 · t(ºC) + 32

donde t(ºF) representa la temperatura expresada en grados Fahrenheit y t(ºC) la expresada en grados Celsius o centígrados.

Escala Kelvin

La escala de temperaturas adoptada por el SI es la llamada escala absoluta o Kelvin. En ella el tamaño de los grados es el mismo que en la Celsius, pero el cero de la escala se fija en el - 273,16 ºC. Este punto llamado cero absoluto de temperaturas es tal que a dicha temperatura desaparece la agitación molecular, por lo que, según el significado que la teoría cinética atribuye a la magnitud temperatura, no tiene sentido hablar de valores inferiores a él. El cero absoluto constituye un límite inferior natural de temperaturas, lo que hace que en la escala Kelvin no existan temperaturas bajo cero (negativas). La relación con la escala centígrada viene dada por la ecuación:

T(K) = t(ºC) + 273,16

siendo T(K) la temperatura expresada en grados Kelvin o simplemente en Kelvin.

                         

Teorema de Bernoulli

El teorema de Bernoulli es un caso particular que precisa la aproximación frecuencial de un suceso a la probabilidad p de que este ocurra a medida que se va repitiendo el experimento.

Dados un suceso A, su probabilidad p de ocurrencia, y n pruebas independientes para determinar la ocurrencia o no-ocurrencia de A.
Sea f el número de veces que se presenta A en los nensayos y  un número positivo cualquiera, la probabilidad de que la frecuencia relativa f/ndiscrepe de p en más de (en valor absoluto) tiende a cero al tender n a ∞. Es decir:

                              

           

Teorema de Torricelli:

El teorema de Torricelli o principio de Torricelli es una aplicación del principio de Bernoulli y estudia el flujo de un líquidocontenido en un recipiente, a través de un pequeño orificio, bajo la acción de lagravedad.

La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio.

Matemáticamente: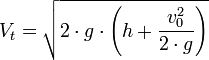

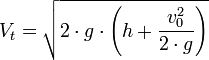
donde:

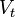•  es la velocidad teórica del líquido a la salida del orificio
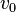•  es la velocidad de aproximación o inicial.
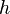•  es la distancia desde la superficie del líquido al centro del orificio.
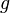•  es la aceleración de la gravedad

Para velocidades de aproximación bajas, la mayoría de los casos, la expresión anterior se transforma en:

              



DILATACIÓN:

Llamamos dilatación al cambio de dimensiones que experimentan los sólidos, líquidos y gases cuando se varía la temperatura, permaneciendo la presión constante. La mayoría de los sistemas aumentan sus dimensiones cuando se aumenta la temperatura.

Dilatación de los sólidos

La dilatación es el cambio de cualquier dimensión lineal del sólido tal como su longitud, alto o ancho, que se produce al aumentar su temperatura. Generalmente se observa la dilatación lineal al tomar un trozo de material en forma de barra o alambre de pequeña sección, sometido a un cambio de temperatura, el aumento que experimentan las otras dimensiones son despreciables frente a la longitud. Si la longitud de esta dimensión lineal es Lo, a la temperatura to y se aumenta la temperatura a t, como consecuencia de este cambio de temperatura, que llamaremos Δt se aumenta la longitud de la barra o del alambre produciendo un incremento de longitud simbolizaremos como ΔL Experimentalmente se encuentra que el cambio de longitud es proporcional al cambio de temperatura y la longitud inicial. Lo. Podemos entonces escribir:

ΔL ∝ Lo. Δt

o bien que

ΔL =αot. Lo. Δt